粗略DL自阅笔记——CNN
怕忘记,所以写下来给自己看,很粗略,只是为了提醒自己某些关键点
主要参考李宏毅老师的课程和邱锡鹏老师的书
为什么要用CNN?
在识别图像的时候,图像在计算机用pixel存储,一个彩色图像假设是100✖️100,由于是彩色需要加上3个维度,则有30000个pixel,如果用传统的全连接神经网络去做分类,那么需要学习整个的30000个参数,参数过多了。而其中很多参数是不必要的。
为什么可以减少参数?图像的特点
第一点,对于一张图片而言,并不需要识别整张图片,只需要识别其中的部分特征即可,比如识别鸟,只需要识别鸟嘴,羽毛等等,而对于图片背景,则是无关紧要的。
第二点,同样的pattern可能出现在图的不同位置,可以用同样的侦测方式去识别,公用同一组参数。
第三点,对于图像而言,av画质和高清画质,人依然可以分辨出是同一种东西。
第一点和第二点CNN的卷积(Convolution)完成,第三点由池化完成。
CNN结构
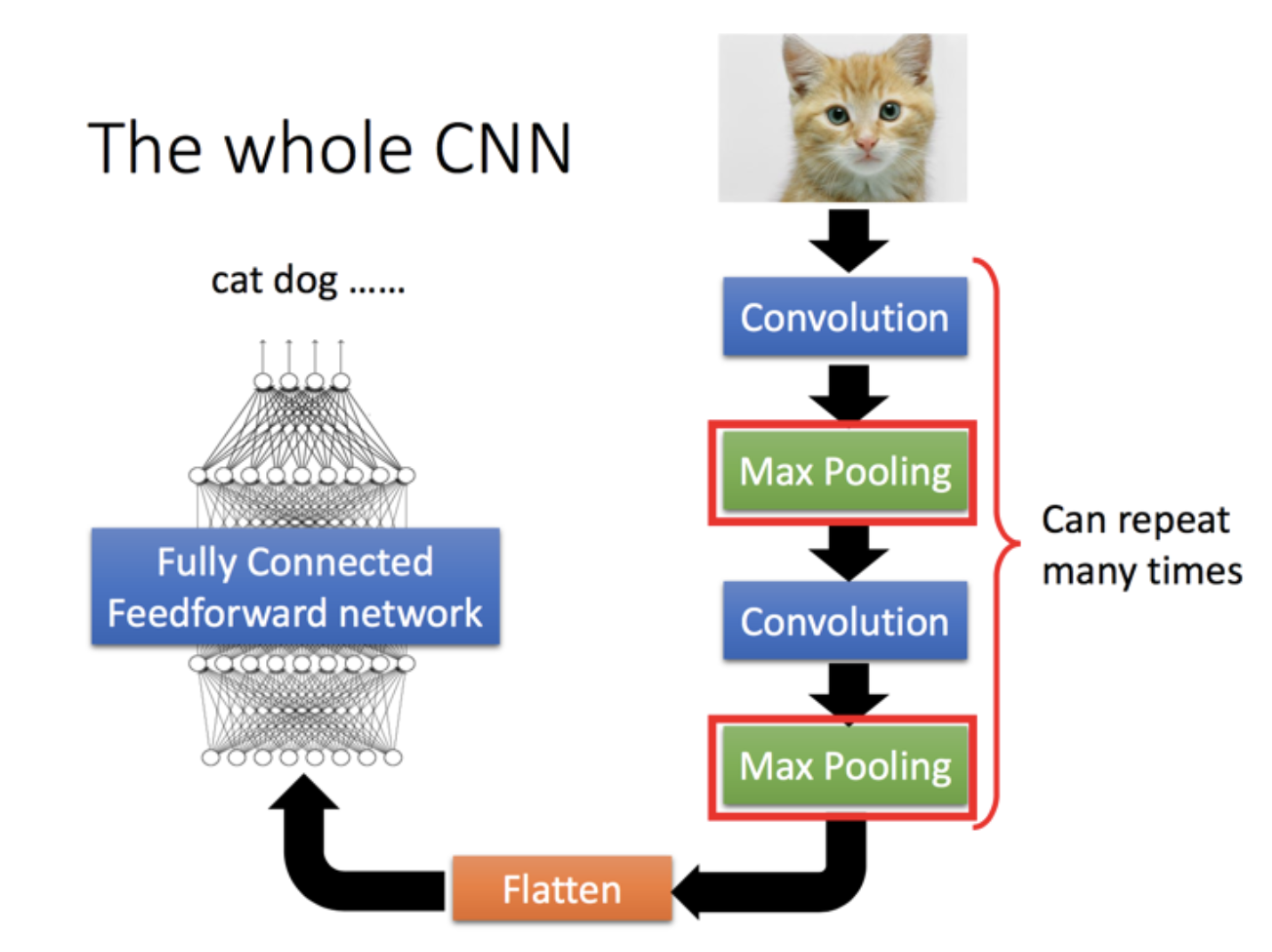
###卷积Convolution
卷积层通过filter提取特征,输出特征映射图feature map
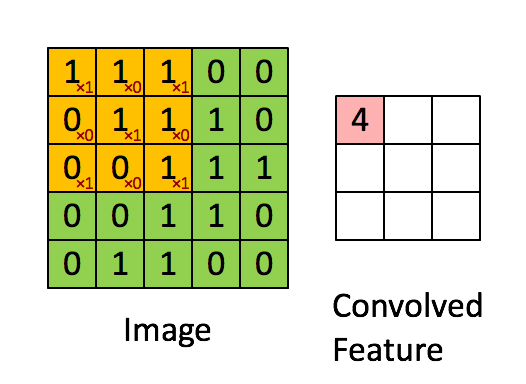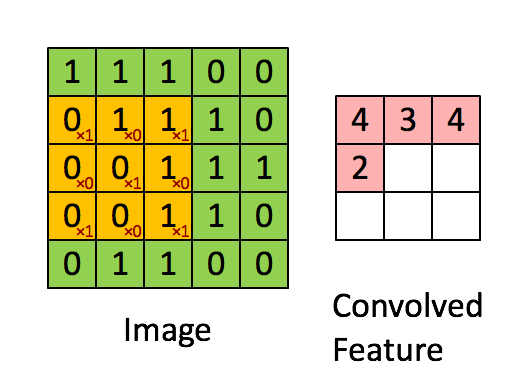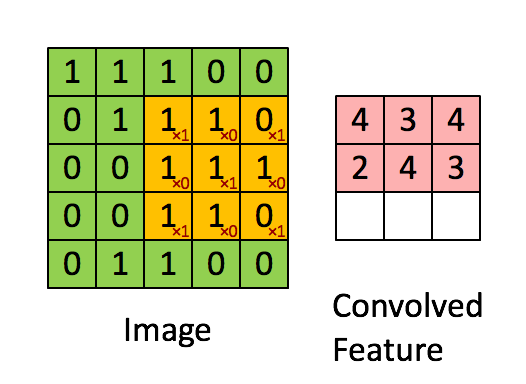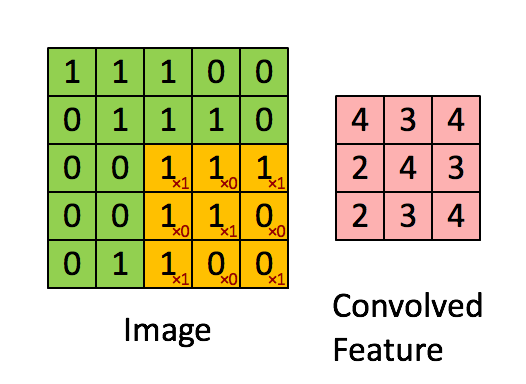
每层的卷积运算即用filter与image做内积
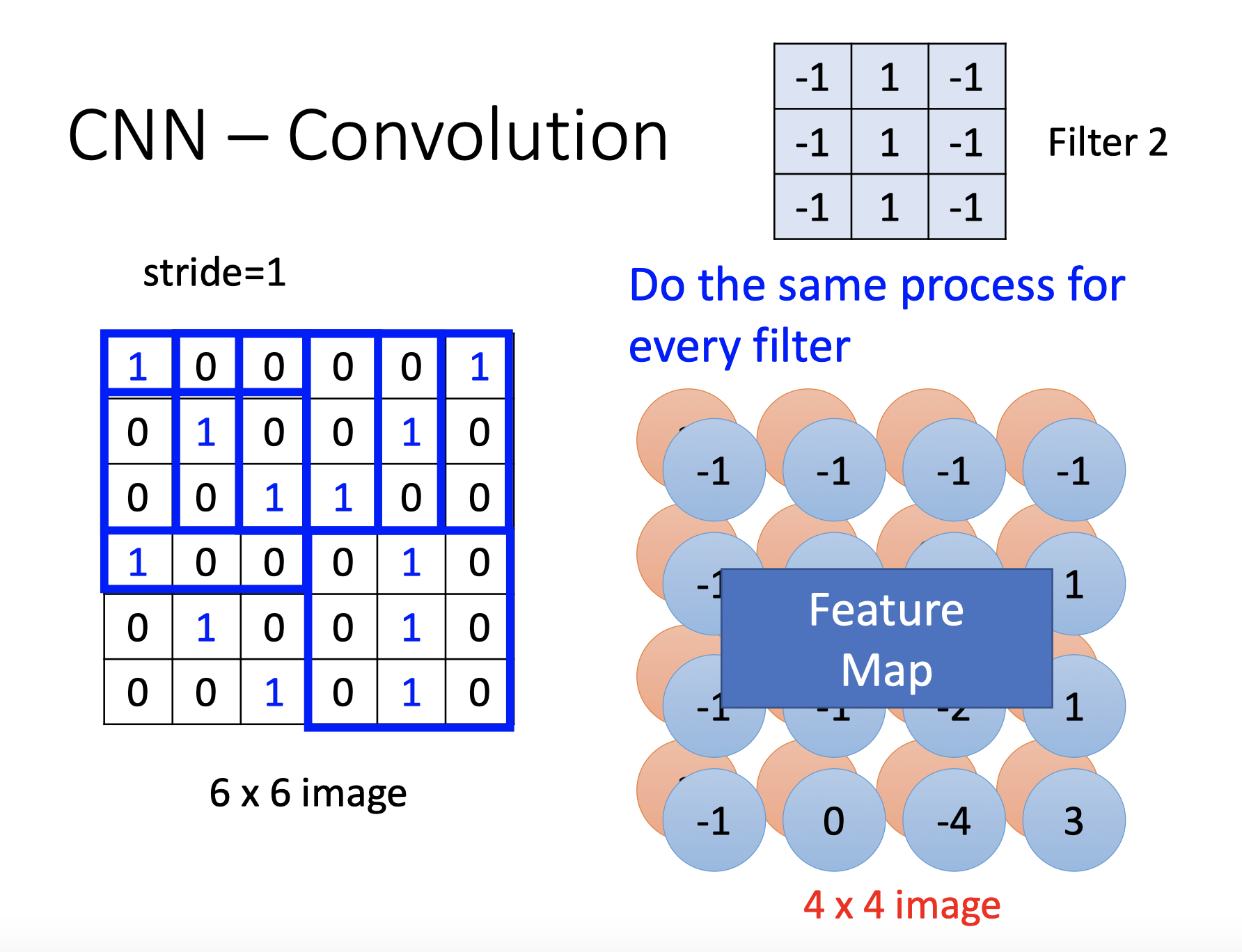
filter可以视为dnn的参数(即神经网络的“边”),原本的图像为input,filter与input内积为output
filter共享相同的参数,一个filter对图片进行一次扫描得到一层的feature map(每个输出的特征映射都需要一个filter和一个偏置),可以设置多个filter,得到多层的feature map,filter移动的距离也可以进行设置
由于相同的filter是一样的参数,这样就减少了参数
这里有一个疑问是,第二层的卷积和池化,是否会让feature map的维度以指数倍增长,不会,因为第二层的filter可以设置为立方的。比如经过第一次的一个平面的filter之后,channel变味了25,那第二层的卷积的filter可以考虑深度为25,并非直接是一个平面。
有一个说法是,卷积层虽然可以显著减少连接的个数,但是每一个特征映射的神经元个数并没有显著减少。这个意思是filter因为共享的缘故,减少了参数,但是由于多个filter,使得下一层的output仍然很多。
在实际操作中,加入非线性结构可以有助于防止过拟合,故典型CNN结构可以是这样

步幅
卷积中的过滤器filter,若设置为1,接受域会有很大的重叠,如果想让接受域重叠少且更小的空间维度,可以考虑增加步幅
填充padding
填充即在过滤器filter边界填充0元素,在网络的早期层中,我们想要尽可能多地保留原始输入内容的信息,这样我们就能提取出那些低层的特征。比如说我们想要应用同样的卷积层,但又想让输出量维持为 32 x 32 x 3 。为做到这点,我们可以对这个层应用大小为 2 的零填充(zero padding)。零填充在输入内容的边界周围补充零。如果我们用两个零填充,就会得到一个 36 x 36 x 3 的输入卷。
如果你的步幅为 1,而且把零填充设置为
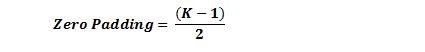
K 是过滤器尺寸,那么输入和输出内容就总能保持一致的空间维度。
计算任意给定卷积层的输出的大小的公式是
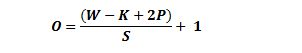
其中 O 是输出尺寸,K 是过滤器尺寸,P 是填充,S 是步幅。
这一节的描述来自[机器之心的知乎回答][https://www.zhihu.com/question/52668301?sort=created]
池化Pooling
卷积层虽然可以显著减少网络中权重的数量,但特征映射组中的神经元个数并没有显著减少
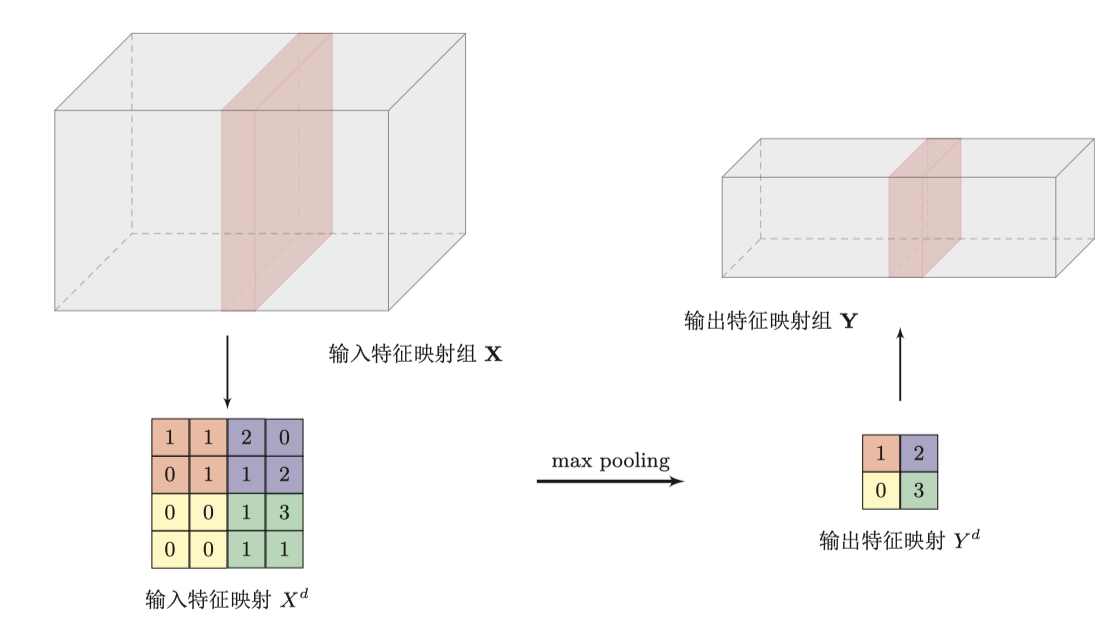
池化可以有效的减少神经元个数,对应图像特点的第三点(减少图像pixel个数),将卷积层得到的feature map用最大值下采样或平均值下采样等方式得到更少的参数
Flatten
Flatten即把最后一次池化后的结果,tensor,给拉直,作为全连接神经网络的输入
参数学习
在全连接神经网络中,采用反向传播算法,因为链式求导,很容易优化参数(神经元之间连接边的权重),使损失函数最小化
CNN中仍是使用反向传播,不过由于卷积和池化,误差项𝛿的计算会有所不同
池化层
在前向传播时,若后一层时池化层,则会采取下采样的操作,一般为取最大MAX或者求平均Average,为了求L层的误差项,需要对L+1层的误差项进行上采样(upsample)
这样便可以得到后一层的 ,由于池化层没有参数需要学习,使用的是线性激活函数,故
,由于池化层没有参数需要学习,使用的是线性激活函数,故
.gif)
卷积层
回顾卷积层前向传播公式,其中å^(l-1)是卷积层的输入,å^(l)是输出
.gif)
根据DNN,求该层的 是关键,而层与层之间进行传播
是关键,而层与层之间进行传播
.gif)
可以得到
.gif)
这里对比层与层之间的递推传播
DNN:.gif)
池化层:.gif)
卷积层:.gif)
这一节可以参考[刘建平的博客][https://www.cnblogs.com/pinard/p/6494810.html#!comments]和[legend_hua的博客][https://blog.csdn.net/legend_hua/article/details/81590979]
一些经典网络结构
这一节内容待补充
LeNet-5
AlexNet
###VGG
ResNet
Inception网络
卷积神经网络的应用
CNN最初更多的是用来CV上的任务,但由于其本身卷积在频域上的平移不变性,同时VGG,ResNet等深度CNN的提出,使之在语音识别,nlp上也有一些热门的应用。
待补充
DNN/CNN的不足
- 连接存在层与层之间,每层的节点之间是无连接的
- 输入和输出的维数都是固定的,不能任意改变,无法处理变长的序列数据
- 假设每次输入都是独立的,即每次网络的输出只依赖于当前的输入